Direction Angles, Cosines and Direction Ratios

Consider two lines whose direction ratios are $\left(2, -1, 2\right)$ and $\left(k, 3, 5\right)$. They are inclined at an angle $\frac{\pi }{4}$.

What are the direction ratios of a line which is perpendicular to both the lines?

Consider two lines whose direction ratios are $\left(2, -1, 2\right)$ and $\left(k, 3, 5\right)$. They are inclined at an angle $\frac{\pi }{4}$.

What is the value of $k$?

Let a line $L$ pass through the origin and be perpendicular to the lines $L_1:\overrightarrow{r}=\left(\hat{i}-11\hat{j}-7\hat{k}\right)+\lambda \left(\hat{i}+2\hat{j}+3\hat{k}\right), \lambda \in \mathrm{ℝ}$ and
$L_2:\overrightarrow{r}=\left(-\hat{i}+\hat{k}\right)+\mu \left(2\hat{i}+2\hat{j}+\hat{k}\right), \mu \in \mathrm{ℝ}$. If $P$ is the point of intersection of $L$ and $L_1$, and $$,$Q\left(\alpha ,\beta ,\gamma \right)$ is the foot of perpendicular from $P$ on $L_2$, then $9\left(\alpha +\beta +\gamma \right)$ is equal to ________.

Let $P\left(-2,-1,1\right)$ and $Q\left(\frac{56}{17}, \frac{43}{17}, \frac{111}{17}\right)$ be the vertices of the rhombus $PQRS.$ If the direction ratios of the diagonal $RS$ are $\alpha ,-1,\beta$, where both $\alpha \text{and} \beta$ are integers of minimum absolute values, then ${\alpha }^2+{\beta }^2$ is equal to $$

If direction ratios of a line are $\lambda , \sqrt{{\lambda }^2-3},1$ and it makes and angle of ${60}^{\circ }$ with $z-$axis, then a value of $y$ is $?$

 Which of the following statement is true?

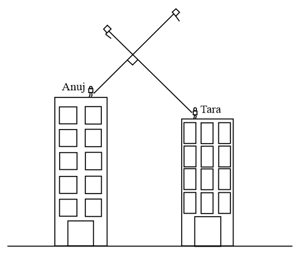
Anuj and Tara are flying kites from their rooftops. Anuj's kite's string is represented by a straight line, given by $\frac{x-4}{1}=\frac{y-2}{3}=\frac{z-1}{2}.$ Tara's position is at $\left(2\hat{i}-2\hat{j}+\hat{k}\right),$ and her kite's string is perpendicular to Anuj's. Find out how far Tara is from where the kite strings intersect. Show your work.

A line makes an angle of 135° with the positive direction of the x-axis, and an angle of 300° with the positive direction of the y-axis.   Which of the following could be the angle it makes with the negative direction of the z axis? 

Write the direction cosines of the line, whose Cartesian equations are $6x-12=3y+9=2z-2.$

If $\overrightarrow{a}=\frac{1}{\sqrt{4}}\left(2\hat{i}+3\hat{j}+\hat{k}\right)$ then write the direction cosines of $\overrightarrow{a}$ ?

The direction ratios of a normal to the plane passing through $(0,1,1),(1,1,2)$ and $(-1,2,-2)$ are

A line is inclined at an angle $\alpha , \beta , \gamma$ with the positive direction of $x, y, z$ axes respectively. If $\beta +\gamma =\frac{\mathrm{\pi }}{2}$, then the maximum possible value of ${\left(\cos \alpha +\sin \beta +\sin \gamma \right)}^2$ is equal to

$\overrightarrow{r}=5\hat{i}-2\hat{j}+3\hat{k}+\lambda \left(2\hat{i}+\hat{j}+\hat{k}\right)$ and $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+3}{1}.$ Find the angle between $2$ lines.

The angle between the pair of lines $\frac{x+3}{3}=\frac{y-1}{5}=\frac{z+3}{4}$ and $\frac{x+1}{1}=\frac{y-4}{4}=\frac{z-5}{2}$ is

Let $A=\left(3,4,0\right), B=\left(4,4,4\right),C=\left(-6,2,3\right)$ and $D=\left(1,1,2\right)$. If $\theta$ is the acute angle between the lines $AB$ and $CD$ then $\cos \theta =$

If $\left(2,3,c\right)$ are the direction ratios of a ray passing through the point $C\left(5,q,1\right)$ and also the mid point of the line segment joining the points $A\left(p,-4.2\right)$ and $B\left(3,2,-4\right)$ then $c.\left(p+7q\right)=$

If $\left(a,b,c\right)$ are the direction ratios of a line joining the points $\left(4,3,-5\right)$ and $\left(-2,1,-8\right)$ then the point $P\left(a,3 b,2c\right)$ lies on the plane

If $\theta$ is angle between the lines $\frac{x}{1}=\frac{y+1}{2}=\frac{z-1}{3}$ and $\frac{x+1}{3}=\frac{y}{2}=\frac{z}{1}$, then $\cos \theta =$

If the direction ratios of a line are $1,-3,2$, then the direction cosines of the line are

If the direction ratios $a, b, c$ of a line $L$ satisfy the relation $ab+bc+ca=0$ and $6ab+9bc+8ca=0$, then the direction cosines of the line $L$ are